Ncert Exercises & Solutions

4.35. A cricket fielder can throw the cricket ball with a speed $v_{0}$ . If he throws the ball while running with speed u at an angle θ to the horizontal, find

a) the effective angle to the horizontal at which the ball is projected in the air as seen by a spectator

b) what will be the time of flight?

c) what is the distance from the point of projection at which the ball will land?

d) find θ at which he should throw the ball that would maximize the horizontal range as found c)

e) how does θ for maximum range change if $u > u_{0}, u = u_{0}, u < v_{0}$ ?

f) how does θ in e) compare with that for u = 0 $(i . e ., 45^{\circ})$ ?

Hint: Horizontal velocity of the ball is added with the velocity of man.

Step 1: Find the net velocity of the ball seen by the spectator.

Consider the adjacent diagram.

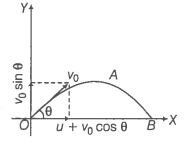
(a) Initial velocity in
$\begin{array}{l} x -direction, u_{x} = u + v_{0} cosθ \\ u_{y} = Initial velocity in y -direction \\ = v_{0} sinθ \end{array}$

where the angle of projection is $θ$ .
Now, we can write

$\begin{array}{l} \tan θ = \frac{u_{y}}{u_{x}} = \frac{u_{0} \sin θ}{u + u_{0} \cos θ} \\ \Rightarrow θ = \tan^{- 1} (\frac{v_{0} \sin θ}{u + v_{0} \cos θ}) \end{array}$

Step 2: Find the time of flight

(b) Let T be the time of flight.
As net vertical displacement is zero over the time period T
$y = 0, u_{y} = v_{0} sinθ, a_{y} = - g, t = T$
We know that $y = u_{y} t + \frac{1}{2} a_{y} t^{2}$

$\begin{array}{l} \Rightarrow 0 = v_{0} \sin θT + \frac{1}{2} (- g) T^{2} \\ \Rightarrow T [v_{0} sinθ - \frac{g}{2} T] = 0 \Rightarrow T = 0, \frac{2 v_{0} \sin θ}{g} \\ T = 0, corresponds to point 0 . \\ Hence, T = \frac{2 u_{0} \sin θ}{g} \end{array}$

Step 3: Find the horizontal range.

(c)

$\begin{array}{l} Horizontal range, R = (u + v_{0} \cos θ) T = (u + v_{0} \cos θ) \frac{2 v_{0} \sin θ}{g} \\ = \frac{v_{0}}{g} [2 usin θ + v_{0} \sin 2 θ] \end{array}$

Step 4: Apply maxima and minima and find the maximum horizontal ranges for different conditions.

(d)

$For horizontal range to be maximum, \frac{d R}{d θ} = 0$

$\begin{array}{l} \Rightarrow \frac{v_{0}}{g} [2 ucos θ + v_{0} \cos 2 θ \times 2] = 0 \\ \Rightarrow 2 ucos θ + 2 v_{0} [2 \cos^{2} θ - 1] = 0 \\ \Rightarrow 4 v_{0} \cos^{2} θ + 2 ucos θ - 2 v_{0} = 0 \\ \Rightarrow 2 v_{0} \cos^{2} θ + ucos θ - v_{0} = 0 \\ \Rightarrow \cos θ = \frac{- u \pm \sqrt{u^{2} + 8 v_{0}^{2}}}{4 v_{0}} \\ \Rightarrow θ_{\max} = \cos^{- 1} [\frac{- u \pm \sqrt{u^{2} + 8 v_{0}^{2}}}{4 v_{0}}] \\ = \cos^{- 1} [\frac{- u + \sqrt{u^{2} + 8 v_{0}^{2}}}{4 v_{0}}] \end{array}$

(e) If $u = v_{0}$

$\cos θ = \frac{- v_{0} \pm \sqrt{v_{0}^{2} + 8 v_{0}^{2}}}{4 v_{0}} = \frac{- 1 + 3}{4} = \frac{1}{2}$
$\Rightarrow θ = 60^{\circ}$
$\begin{array}{l} If u << v_{0}, then 8 v_{0}^{2} + u^{2} \approx 8 v_{0}^{2} \\ \begin{matrix} θ_{\max} = \cos^{- 1} [\frac{- u \pm 2 \sqrt{2} v_{0}}{4 v_{0}}] = \cos^{- 1} [\frac{1}{\sqrt{2}} - \frac{u}{4 v_{0}}] \\ θ_{\max} = \cos^{- 1} [\frac{1}{\sqrt{2}}] = \frac{π}{4} \\ u >> v_{0} \\ θ_{\max} = \cos^{- 1} [\frac{- u \pm u}{4 v_{0}}] = 0 \Rightarrow θ_{\max} = \frac{π}{2} \end{matrix} \end{array}$

(f) If $u = 0, θ_{\max} = \cos^{- 1} [\frac{0 \pm \sqrt{8 v^{2} 0}}{4 v_{0}}] = \cos^{- 1} (\frac{1}{\sqrt{2}}) = 45^{\circ}$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions