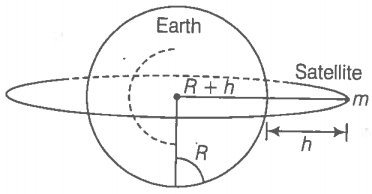
Hint: A geostationary satellite is a satellite that revolves with the rotation of the earth.
Consider the adjacent diagram.
Given, the mass of the earth M =
The radius of the earth, R = 6400 km =
Time period, T = 24 h = 24x60x60 = 86400 sec
Step 1: Find the height of the satellite.
(a) Time period,
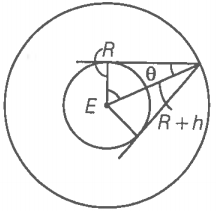
Step 2: Find the no. of satellites.
(b) If the satellite is at height h from the earth’s surface, then according to the diagram:
If n is the number of satellites needed to cover the entire earth, then:
Minimum 3 satellites are required to cover the entire earth.