Distance of the centre of mass of a solid uniform cone from its vertex is \(Z_0\). If the radius of its base is \(R\) and its height is \(h\) then \(Z_0\) is equal to:
1. \( \frac{{h}^2}{4{R}} \)
2. \(\frac{3 h}{4} \)
3. \(\frac{5 h}{8} \)
4. \(\frac{3{h}^2}{8{R}}\)
1. \({a=2b}\)
2. \({2a=b}\)
3. \({a=b}\)
4. \({3a=2b}\)
A uniform rectangular thin sheet \(ABCD\) of mass \(M\) has length \(a\) and breadth \(b.\) If the shaded portion \(HBGO\) is removed, the coordinates of the centre-of-mass of the remaining portion will be:
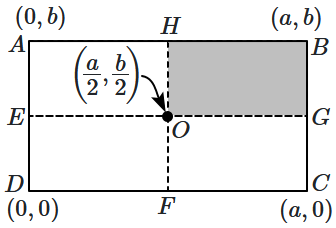
| 1. | \( \left(\dfrac{5 a}{3}, \dfrac{5 b}{3}\right) \) | 2. | \( \left(\dfrac{2 a}{3}, \dfrac{2 b}{3}\right) \) |
| 3. | \( \left(\dfrac{5 a}{12}, \dfrac{5 b}{12}\right) \) | 4. | \( \left(\dfrac{3 a}{4}, \dfrac{3 b}{4}\right) \) |
A man (mass = \(50\) kg) and his son (mass = \(20\) kg) are standing on a frictionless surface facing each other. The man pushes his son so that he starts moving at a speed of \(0.70~\text{ms}^{-1}\) with respect to the man. The speed of the man with respect to the surface is:
1. \(0.28~\text{ms}^{-1}\)
2. \(0.47~\text{ms}^{-1}\)
3. \(0.20~\text{ms}^{-1}\)
4. \(0.14~\text{ms}^{-1}\)
Three particles of masses \(100~\text{g}\), \(150~\text{g}\), and \(200~\text{g}\) respectively are placed at the vertices of an equilateral triangle of a side \(0.5~\text{m}\) long. What is the position of the centre of mass of three particles?

| 1. | \(\left(\dfrac{5}{18} , \dfrac{1}{3 \sqrt{3}}\right) \) | 2. | \(\left(\dfrac{1}{4} , 0\right) \) |
| 3. | \(\left(0 , \dfrac{1}{4}\right) \) | 4. | \(\left(\dfrac{1}{3 \sqrt{3}} , \dfrac{5}{18}\right) \) |
A square shaped hole of side \(l=\dfrac{a}{2}\) is carved out at a distance \(d=\dfrac{a}{2}\) from the centre '\(O\)' of a uniform circular disk of radius \(a\). If the distance of the centre of mass of the remaining portion from \(O\) is \(-\dfrac{a}{x}\) value of \(x\) (to the nearest integer) is:
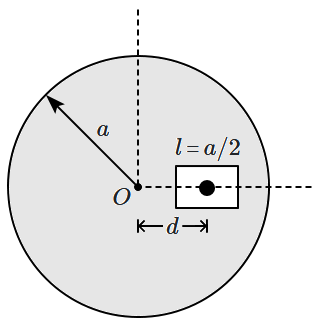
1. \(12\)
2. \(23\)
3. \(45\)
4. \(76\)
The centre-of-mass of a solid hemisphere of radius \(8\) cm is located at a distance of \(x\) cm from the centre of its flat circular surface. The value of \(x\) is:
1. \(3\)
2. \(7\)
3. \(9\)
4. \(1\)
A circular hole of radius \(\dfrac{a}{2}\) is cut out of a circular disc of radius, \(a\) as shown in the figure. The centroid (centre-of-mass) of the remaining circular portion with respect to the point, \(O\) will be:
| 1. | \(\dfrac{1}{6}a\) | 2. | \(\dfrac{10}{11}a\) |
| 3. | \(\dfrac{5}{6}a\) | 4. | \(\dfrac{2}{3}a\) |
Two masses \(A\) and \(B,\) each of mass \(M\) are fixed together by a massless spring. A force acts on the mass \(B\) as shown in the figure. If mass \(A\) starts moving away from mass \(B\) with acceleration \(a,\) then the acceleration of mass \(B\) will be:

| 1. | \( \frac{M a-F}{M} \) | 2. | \(\frac{M F}{F+M a} \) |
| 3. | \(\frac{F+M a}{M} \) | 4. | \(\frac{F-M a}{M} \) |
| 1. | \(4~\text{cm}\) towards the \(10~\text{kg}\) block |
| 2. | \(2~\text{cm}\) away from the \(10~\text{kg}\) block |
| 3. | \(2~\text{cm}\) towards the \(10~\text{kg}\) block |
| 4. | \(4~\text{cm}\) away from the \(10~\text{kg}\) block |







