- 1(current)
Q. No.The elastic behaviour of a material for linear stress and linear strain is captured in the graph below. The energy density, for a linear strain of \(5 \times 10^{-4} \) is:
\((\)assume that the material is elastic up to the linear strain of \(5 \times 10^{-4})\)
\((\)assume that the material is elastic up to the linear strain of \(5 \times 10^{-4})\)
| 1. | \(15\) kJ/m3 | 2. | \(20\) kJ/m3 |
| 3. | \(25\) kJ/m3 | 4. | \(30\) kJ/m3 |
Subtopic: Â Stress - Strain Curve |
 76%
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
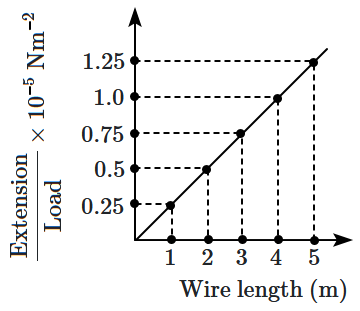
In an experiment to determine Young's modulus, steel wires of five different lengths ( \(1,2,3,4\) and \(5~\text m\) ) but of the same cross-section (\(2~\text{mm}^2\)) were taken and curves between extension and load were obtained. The slope (extension/load) of the curves was plotted with the wire length and the following graph is obtained. If Young's modulus of a given steel wire is \(x\times 10^{11}~\text{N/m}^2,\) then the value of \(x\) is:
1. \(1\)
2. \(2\)
3. \(3\)
4. \(4\)
1. \(1\)
2. \(2\)
3. \(3\)
4. \(4\)
Subtopic: Â Stress - Strain Curve |
 74%
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
- 1(current)
Q. No.
© 2025 GoodEd Technologies Pvt. Ltd.