Select Chapter Topics:
For an electron and a proton \((m_p = 1847 m_e)\) with same de-Broglie wavelength, the ratio of linear momentum is equal to:
1. \(1:2\)
2. \(2: 1847\)
3. \(1:1\)
4. \(\sqrt{1847} :1\)
Subtopic: De-broglie Wavelength |
81%
Level 1: 80%+
JEE
Please attempt this question first.
Hints
Please attempt this question first.
If the de-Broglie wavelength is \(\lambda,\) when the energy is \(E,\) what will the wavelength be when the energy is \(\dfrac{E}{4}\) (kinetic energy)?
| 1. | \(2\lambda\) | 2. | \(\sqrt{2}\lambda\) |
| 3. | \(\lambda\) | 4. | \(\dfrac{\lambda}{\sqrt{2}}\) |
Subtopic: De-broglie Wavelength |
81%
Level 1: 80%+
JEE
Please attempt this question first.
Hints
Please attempt this question first.
Two different photosensitive materials have work function \(\phi\) and \(2\phi\) respectively, are illuminated with light of sufficient energy to emit electrons. If the graph of stopping potential versus frequency is drawn, for these two different photosensitive materials, the ratio of the slope of the graph for these two materials is:
1. \(1:1\)
2. \(1:2\)
3. \(1:4\)
4. \(4:1\)
1. \(1:1\)
2. \(1:2\)
3. \(1:4\)
4. \(4:1\)
Subtopic: Einstein's Photoelectric Equation |
74%
Level 2: 60%+
JEE
Please attempt this question first.
Hints
Please attempt this question first.
The radius of the first orbit in a hydrogen atom is \(a_0.\) The de-Broglie wavelength of the electron in the third orbit is:
\(\begin{align} & {{1}{.}\;{3}\mathit{\pi}{a}_{0}}\\ & {{2}{.}\;{6}\mathit{\pi}{a}_{0}}\\ & {{3}{.}\;{9}\mathit{\pi}{a}_{0}}\\ & {{4}{.}\;{12}\mathit{\pi}{a}_{0}} \end{align} \)
\(\begin{align} & {{1}{.}\;{3}\mathit{\pi}{a}_{0}}\\ & {{2}{.}\;{6}\mathit{\pi}{a}_{0}}\\ & {{3}{.}\;{9}\mathit{\pi}{a}_{0}}\\ & {{4}{.}\;{12}\mathit{\pi}{a}_{0}} \end{align} \)
Subtopic: De-broglie Wavelength |
60%
Level 2: 60%+
JEE
Please attempt this question first.
Hints
Please attempt this question first.
Kinetic energy of electron, proton and \(\alpha\)-particle is given as k, 2k and 4k respectively then which of the following gives the correct order of de-Broglie wavelength of electron, proton and \(\alpha\)-particle?
1. \(\lambda_{p}>\lambda_{\alpha}>\lambda_{e}\)
2. \(\lambda_{\alpha}>\lambda_{p}>\lambda_{e}\)
3. \(\lambda_{e}>\lambda_{p}>\lambda_{\alpha}\)
4. \(\lambda_{e}>\lambda_{\alpha}>\lambda_{p}\)
1. \(\lambda_{p}>\lambda_{\alpha}>\lambda_{e}\)
2. \(\lambda_{\alpha}>\lambda_{p}>\lambda_{e}\)
3. \(\lambda_{e}>\lambda_{p}>\lambda_{\alpha}\)
4. \(\lambda_{e}>\lambda_{\alpha}>\lambda_{p}\)
Subtopic: De-broglie Wavelength |
87%
Level 1: 80%+
Please attempt this question first.
Hints
Please attempt this question first.
Based on the given graph between stopping potential, \((V)\) and frequency, \((\nu)\) of irradiation, the work function of the metal is equal to:
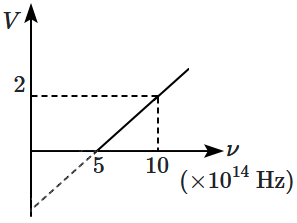
1. \(1\) eV
2. \(3\) eV
3. \(2\) eV
4. \(4\) eV

1. \(1\) eV
2. \(3\) eV
3. \(2\) eV
4. \(4\) eV
Subtopic: Einstein's Photoelectric Equation |
75%
Level 2: 60%+
JEE
Please attempt this question first.
Hints
Please attempt this question first.
Proton and electrons have equal kinetic energy, the ratio of de Broglie wavelength of proton and electron is 1/x . Find x. (Mass of proton = 1849 times mass of electron)
1. 43
2. 56
3. 76
4. 21
1. 43
2. 56
3. 76
4. 21
Subtopic: De-broglie Wavelength |
60%
Level 2: 60%+
Please attempt this question first.
Hints
Please attempt this question first.
The stopping potential for a metal, when illuminated with light of wavelength \(\lambda,\) is \(V_0.\) For light of wavelength \(2 \lambda,\) the stopping potential is \(\dfrac{V_0}{4}.\) The threshold wavelength of the metal is:
| 1. | \(\lambda\) | 2. | \(2\lambda\) |
| 3. | \(3\lambda\) | 4. | \(4\lambda\) |
Subtopic: Einstein's Photoelectric Equation |
73%
Level 2: 60%+
JEE
Please attempt this question first.
Hints
Please attempt this question first.
Find ratio of de-Broglie wavelength of a proton and an \(\alpha-\) particle, when accelerated through a potential difference of 2 V and 4 V respectively
1. \(4 : 1\)
2. \(2 :1\)
3. \(1 : 8\)
4. \(16 : 1\)
1. \(4 : 1\)
2. \(2 :1\)
3. \(1 : 8\)
4. \(16 : 1\)
Subtopic: De-broglie Wavelength |
67%
Level 2: 60%+
Please attempt this question first.
Hints
Please attempt this question first.
If a substance absorbs \(500~\text{nm}\) wavelength radiation and emits radiation of wavelength \(600~\text{nm},\) then the net change in energy is: (take \(hc=1240~\text{eV-nm}\))
1. \(1.2\times10^{-3}~\text{eV}\)
2. \(3.0\times10^{-4}~\text{eV}\)
3. \(4.1\times10^{-1}~\text{eV}\)
4. \(5.2\times10^{-4}~\text{eV}\)
1. \(1.2\times10^{-3}~\text{eV}\)
2. \(3.0\times10^{-4}~\text{eV}\)
3. \(4.1\times10^{-1}~\text{eV}\)
4. \(5.2\times10^{-4}~\text{eV}\)
Subtopic: Particle Nature of Light |
78%
Level 2: 60%+
JEE
Please attempt this question first.
Hints
Please attempt this question first.






