- 1(current)
Q. No.If the absolute temperature of a star doubles but its radius halves, then the rate of radiation from the star:
1. increases \(4\) times
2. increases \(2\) times
3. remains unchanged
4. decreases \(2\) times
1. increases \(4\) times
2. increases \(2\) times
3. remains unchanged
4. decreases \(2\) times
Subtopic: Radiation |
75%
Level 2: 60%+
To unlock all the explanations of this course, you need to be enrolled.
Hints
To unlock all the explanations of this course, you need to be enrolled.
A steel rod, insulated at its sides, is inserted into a high temperature oven – as shown in the figure. The end of the rod is blackened and is observed to be at a temperature \(T_b,\) and the temperature of the surroundings is \(T_S.\) The conductivity of steel is \(K,\) and Stefan's constant is \(\sigma.\) The temperature of the oven is (all temperatures are on absolute scale):
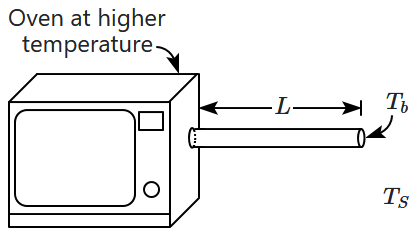
| 1. | \(T_S+\dfrac{L\sigma}{K}T_b^4\) |
| 2. | \(T_b+\dfrac{L\sigma}{K}(T_b-T_S)^4\) |
| 3. | \(T_b+\dfrac{L\sigma}{K}(T_b^4-T_S^4)\) |
| 4. | \(\left\{T_b^4+\dfrac{L\sigma}{K}(T_b^4-T_S^4)\right\}^{1/4}\) |
Subtopic: Radiation |
64%
Level 2: 60%+
To unlock all the explanations of this course, you need to be enrolled.
Hints
To unlock all the explanations of this course, you need to be enrolled.
- 1(current)
Q. No.
© 2025 GoodEd Technologies Pvt. Ltd.