Two identical wires \(\mathrm{A}\) and \(\mathrm{B}\), each of length '\(l\)', carry the same current \(I\). Wire \(\mathrm{A}\) is bent into a circle of radius \(R\) and wire \(\mathrm{B}\) is bent to form a square of side '\(a\)'. If \(B_A\) and \(B_B\) are the values of the magnetic field at the centres of the circle and square respectively, then the ratio \(\frac{B_A}{B_B}\) is? 
1. \( \frac{\pi^2}{8} \)
2. \( \frac{\pi^2}{16 \sqrt{2}} \)
3. \( \frac{\pi^2}{16} \)
4. \( \frac{\pi^2}{8 \sqrt{2}} \)

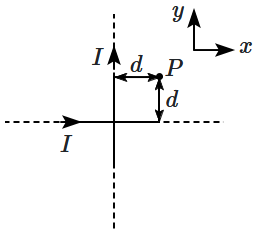
Two very long, straight, and insulated wires are kept at \(90^\circ\) angle from each other in \(xy\text-\)plane as shown in the figure

These wires carry currents of equal magnitude I, whose directions are shown in the figure. The net magnetic field at point \(P\) will be:
1. zero
2. \( -\frac{\mu_0 I}{2 \pi d}(\hat{x}+\hat{y}) \)
3. \( \frac{\mu_0 I}{2 \pi d}(\hat{x}+\hat{y}) \)
4. \( \frac{\mu_0 I}{\pi d}(\hat{z})\)

The magnitude of the magnetic field at the centre of an equilateral triangular loop of side \(1~\text{m}\) which is carrying a current of \(10~\text{A}\) is: [Take \(\mu_0=4 \pi \times 10^{-7} ~\text{NA}^{-2}\)]
1. \( 3~\mu \text{T} \)
2. \(18 ~\mu \text{T} \)
3. \(9~\mu \text{T} \)
4. \(1 ~\mu \text{T} \)

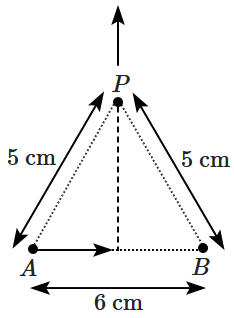
Find the magnetic field at point \(P\) due to a straight line segment \(AB\) of length \(6~\text{cm}\) carrying a current of \(5~\text{A}\). (See figure) (\(\mu_0=4\pi \times 10^{-7}~\text{N-A}^{-2}\))

                               
1. \(1.5\times 10^{-5}~\text{T}\)
2. \(3.0\times 10^{-5}~\text{T}\)
3. \(2.0\times 10^{-5}~\text{T}\)
4. \(2.5\times 10^{-5}~\text{T}\)

Magnitude of magnetic field (in SI units) at the centre of a hexagonal shape coil of side \(10~\text{cm}\), \(50\) turns and carrying current \(I\) (Ampere) in units of \(\frac{\mu_0 I}{\pi}\) is:
1. \(5\sqrt{3}\)
2. \(250\sqrt{3}\)
3. \(50\sqrt{3}\)
4. \(500\sqrt{3}\)

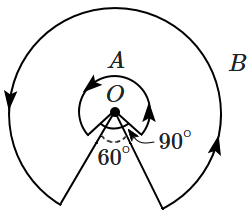
A wire \(A\), bent in the shape of an arc of a circle, carrying a current of \(2~\text{A}\) and having radius \(2\) cm and another wire \(B\), also bent in the shape of arc of a circle, carrying a current of \(3~\text{A}\) and having radius of \(4\) cm, are placed as shown in the figure. The ratio of the magnetic fields due to the wires \(A\) and \(B\) at the common centre \(O\) is:

1. \(6:5\)
2. \(6:4\)
3. \(2:5\)
4. \(4:6\)

Magnetic fields at two points on the axis of a circular coil at a distance of \(0.05~\text m\) and \(0.2~\text m\) from the centre are in the ratio \(8:1.\) The radius of the coil is:
1. \(0.2~\mathrm{m}\)
2. \(0.1~\mathrm{m}\)
3. \(0.15~\mathrm{m}\)
4. \(1.0~\mathrm{m}\)