
1. \({IBR\over 2\sin\theta_0}\)
2. \({IBR\theta_0\over \sin\theta_0}\)
3. \({IBR}\)
4. \({IBR\over \sin\theta_0}\)
| 1. | minimum potential energy when the torque is maximum. |
| 2. | zero potential energy when the torque is minimum. |
| 3. | maximum potential energy when the torque is maximum. |
| 4. | zero potential energy when the torque is maximum. |
| 1. | 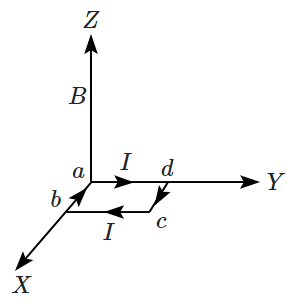 |
3. | 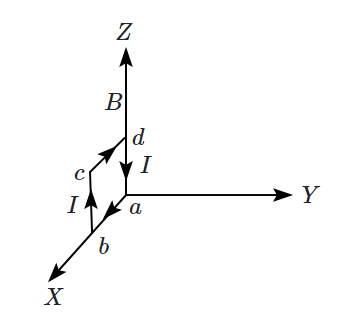 |
| 2. | 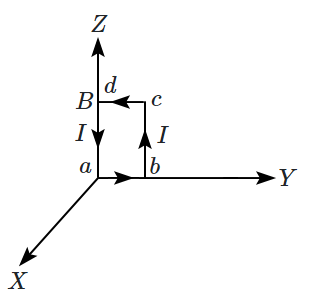 |
4. | 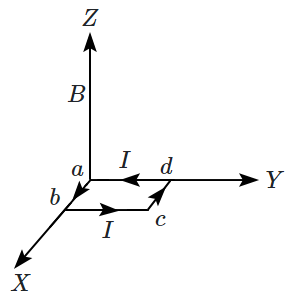 |
A circular coil with \(N\) turns and radius \(r\) carries a current \(I.\) It is held in the \(XZ\)-plane within a magnetic field \(B\hat{i}.\) The torque on the coil due to the magnetic field is:
1. \(\dfrac{B \pi {r}^2 {I}}{N}\)
2. zero
3. \(B \pi {r}^2 {I} {N}\)
4. \(\dfrac{B r^2 I}{\pi {N}}\)
A rectangular coil (Dimension \(5~\text{cm}\times 2.5~\text{cm}\)) with \(100\) turns, carrying a current of \(3~\text{A}\) in the clock-wise direction, is kept centered at the origin and in the \(\mathrm{X\text-Z}\) plane. A magnetic field of \(1~\text{T}\) is applied along \(\mathrm{X\text{-}}\)axis. If the coil is tilted through \(45^\circ\) about \(\mathrm{Z\text{-}}\)axis, then the torque on the coil is:
1. \(0.55~\text{Nm}\)
2. \(0.38~\text{Nm}\)
3. \(0.42~\text{Nm}\)
4. \(0.27~\text{Nm}\)
A moving coil galvanometer has a coil with \(175\) turns and area \(1~\text{cm}^2\). It uses a torsion band of torsion constant \(10^{-6}\) N-m/rad. The coil is placed in a magnetic field \(B\) parallel to its plane. The coil deflects by \(1^\circ\) for a current of \(1~\text{mA}\). The value of \(B\) (in Tesla) is approximately:
1. \( 10^{-3} \)
2. \(10^{-1} \)
3. \(10^{-4} \)
4. \(10^{-2} \)
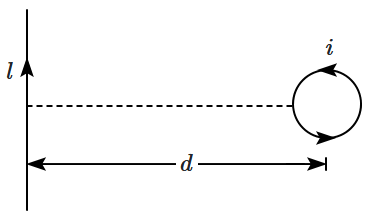
1. \( {F=0} \)
2. \( {F} \propto\left(\dfrac a d\right) \)
3. \( {F} \propto \left(\dfrac{a^2} {d^3} \right) \)
4. \( {F} \propto\left(\dfrac a d\right)^2 \)
A glavanometer coil has \(500\) turns and each turn has an average area of \(3 \times 10^{-4}~\text{m}^2\). If a torque of \(1.5~\text{Nm}\) is required to keep this coil parallel to a magnetic field when a current of \(0.5~\text{A}\) is flowing through it, the strength of the field (in T) is:
1. \(10\)
2. \(40\)
3. \(20\)
4. \(30\)
A square loop of side \(2a\), and carrying current \(I\), is kept in \(XZ\) plane with its centre at origin. A long wire carrying the same current \(I\) is placed parallel to the \(z\text-\)axis and passing through the point (\(0,b,0\)), (\(b >>a\)). The magnitude of the torque on the loop about \(z\text-\)axis is given by:
1. \( \frac{2 \mu_0 I^2 a^2}{\pi b} \)
2. \( \frac{\mu_0 I^2 a^3}{2 \pi b^2} \)
3. \( \frac{\mu_0 I^2 a^3}{2 \pi b} \)
4. \( \frac{2 \mu_0 I^2 a^3}{\pi b^2} \)
A square loop of side \(2a\) and carrying current \(I\) is kept in xz plane with its centre at origin. A long wire carrying the same current \(I\) is placed parallel to z-axis and passing through point (\(0,b,0\)), (\(b>>a\)). The magnitude of torque on the loop about z-axis will be:
1. \( \frac{2 \mu_0 I^2 a^2 b}{\pi\left(\mathrm{a}^2-\mathrm{b}^2\right)} \)
2. \( \frac{\mu_0 I^2 a^2 b}{\pi\left(\mathrm{a}^2-\mathrm{b}^2\right)} \)
3. \( \frac{\mu_0 I^2 a^2}{2 \pi \mathrm{ab}} \)
4. \( \frac{2 \mu_0 I^2 a^2}{\pi \mathrm{b}}\)




