Assume that an electric field \(\vec{E}=30x^2\hat{i}\) exists in space. Then the potential difference \(V_A-V_O\), where \(V_O\) is the potential at the original and \(V_A\) the potential at \(x=2~\text{m}\) is:
1. \(-120~\text{V}\)
2. \(-80~\text{V}\)
3. \(80~\text{V}\)
4. \(120~\text{V}\)

The electric field in a region is given by \(\vec{E}=(A x+B) \hat{i}\), where \(E\) is in \(\text{NC}^{-1}\) and \(x\) is in meters. The value of constants are \(A=20\) SI unit and \(B=10\) SI unit. If the potential at \(x=1\) is \(V_1\) and that at \(x=-5\) is \(V_2\), then \(V_1-V_2\) is:
1. \(-520~\text{V}\)
2. \(180~\text{V}\)
3. \(-48~\text{V}\)
4. \(320~\text{V}\)

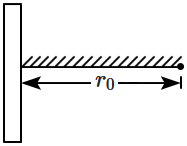
A positive point charge is released from rest at a distance \(r_0\)​ from an infinitely long straight line of positive charge having uniform linear charge density. As the point charge moves directly away from (or toward — depending on sign) the line charge under electrostatic force, its speed \(v\) depends on its instantaneous distance \(r\) from the line charge.

              
The speed \(v\) as a function of \(r,\) is proportional to:
1. \( v \propto e^{+r / r_0} \)
2. \(v \propto \ln \left(\dfrac{r}{r_0}\right ) \)
3. \( v \propto\left(\dfrac{r}{r_0}\right) \)
4. \( v \propto \sqrt{\ln \left(\dfrac{r}{r_0}\right)} \)

Concentric metallic hollow spheres radii \(R\) and \(4R\) hold charges \(Q_1\) and \(Q_2\) respectively. Given that surface charge densities of the concentric spheres are equal, the potential difference \(V(R)-V(4R )\) is:
1. \( \frac{3 Q_1}{16 \pi \varepsilon_0 R} \)
2. \( \frac{3 Q_1}{4 \pi \varepsilon_0 R} \)
3. \( \frac{Q_2}{4 \pi \varepsilon_0 R} \)
4. \( \frac{3 Q_2}{4 \pi \varepsilon_0 R}\)