Select Question Set:
Q. No.Given below is the probability density graph of an orbital.
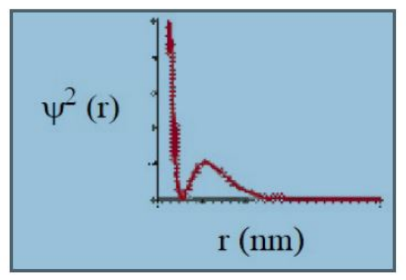
The above graph represents the orbital:
1. 1s
2. 2s
3. 2p
4. 3s
Subtopic: Quantum Numbers & Schrodinger Wave Equation |
64%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
Match List-I with List-II:
Choose the correct answer from the options given below:
| List-I (quantum number) |
List-II (Orbital) |
||
| (A) | n = 2, \(\ell\) = 1 | (I) | 2s |
| (B) | n = 3, \(\ell\) = 2 | (II) | 3s |
| (C) | n = 3, \(\ell\) = 0 | (III) | 2p |
| (D) | n = 2, \(\ell\) = 0 | (IV) | 3d |
Choose the correct answer from the options given below:
| (A) | (B) | (C) | (D) | |
| 1. | (III) | (IV) | (I) | (II) |
| 2. | (IV) | (III) | (I) | (II) |
| 3. | (IV) | (III) | (II) | (I) |
| 4. | (III) | (IV) | (II) | (I) |
Subtopic: Shell & Subshell |
83%
From NCERT
NEET - 2022
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
When electromagnetic radiation of wavelength 300 nm falls on the surface of a metal, electrons are emitted with the kinetic energy of 1.68 × 105 J mol–1. The minimum energy needed to remove one mole of electron from the metal is:
(h = 6.626 × 10–34 Js, c = 3 × 108 ms–1, NA = 6.022 × 1023 mol–1)
1. 2.31 × 106 J mol–1
2. 3.84 × 104 J mol–1
3. 3.84 × 10–19 J mol–1
4. 2.31 × 105 J mol–1
(h = 6.626 × 10–34 Js, c = 3 × 108 ms–1, NA = 6.022 × 1023 mol–1)
1. 2.31 × 106 J mol–1
2. 3.84 × 104 J mol–1
3. 3.84 × 10–19 J mol–1
4. 2.31 × 105 J mol–1
Subtopic: Photo Electric Effect |
From NCERT
NEET - 2022
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
The threshold frequency \((\nu_0)\) for metal is \(6.0 × 10^{14}~\text {sec}^{-1}\). When radiation of frequency, \(\nu = 1.0 × 10^{15}~\text {sec}^{-1} \) hits the metal, the kinetic energy of the electron emitted is:
[Given: h = 6.62 × 10-34 Js]
1. 3.65 × 10–19 J
2. 2.65 × 10–19 J
3. 1.95 × 10–19 J
4. 2.95 × 10–20 J
[Given: h = 6.62 × 10-34 Js]
1. 3.65 × 10–19 J
2. 2.65 × 10–19 J
3. 1.95 × 10–19 J
4. 2.95 × 10–20 J
Subtopic: Photo Electric Effect |
81%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
Which of the following pair of d-orbitals has zero electron density along the axis?
1. \(d_\text {xy} ~\text{and}~ d_ {{\text x^2} -{\text y^2} } \)
2. \(d_\text {yz} ~\text{and}~d_{z^2} \)
3. \( d_ {{\text x^2} -{\text y^2}} ~\text{and} ~d_{z^2} \)
4. \(d_\text {xy} ~\text{and}~d_\text {yz} \)
1. \(d_\text {xy} ~\text{and}~ d_ {{\text x^2} -{\text y^2} } \)
2. \(d_\text {yz} ~\text{and}~d_{z^2} \)
3. \( d_ {{\text x^2} -{\text y^2}} ~\text{and} ~d_{z^2} \)
4. \(d_\text {xy} ~\text{and}~d_\text {yz} \)
Subtopic: Nodal Plane |
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
Lyman series of hydrogen atom falls in which of the following region of the electromagnetic spectrum?
1. Microwave
2. Ultraviolet
3. Visible
4. Infrared
1. Microwave
2. Ultraviolet
3. Visible
4. Infrared
Subtopic: Type of Spectra |
89%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
The correct statement among the following is/are:
1. (III) only
2. (I) and (III) only
3. (II) and (III) only
4. (I), (II) and (III)
| (I). | \( |\Psi|^2 \) is known as a probability density. |
| (II). | The Schrödinger equation can be easily solved for a multi-electron atom. |
| (III). | An atomic orbital is the wave function \( \Psi\) for an electron in an atom. |
1. (III) only
2. (I) and (III) only
3. (II) and (III) only
4. (I), (II) and (III)
Subtopic: Quantum Numbers & Schrodinger Wave Equation |
59%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
Using the following statements, identify the correct set of statements:
1. (i), (ii), (iii)
2. (i), (ii), (iv)
3. (i), (ii), (iii), (iv)
4. (i), (iii), (iv)
| (i). | n (principal quantum number) can have values 1, 2, 3, 4, ....... |
| (ii). | The number of orbitals for a given value of l is (2l+1). |
| (iii). | The value of spin quantum numbers is always \(\pm\frac12\). |
| (iv). | For l=5, the total number of orbitals is 9. |
1. (i), (ii), (iii)
2. (i), (ii), (iv)
3. (i), (ii), (iii), (iv)
4. (i), (iii), (iv)
Subtopic: Quantum Numbers & Schrodinger Wave Equation |
85%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
| Assertion (A): | Helium and berylium having the similar outer electronic configuration of type \(ns^2\). |
| Reason (R): | Both are chemically inert. |
| 1. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. | (A) is True but (R) is False. |
| 4. | Both (A) and (R) are False. |
Subtopic: AUFBAU Principle |
68%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
| Assertion (A): | Half-filled and fully-filled degenerate orbitals are more stable. |
| Reason (R): | Extra stability is due to the symmetrical distribution of electrons and high exchange energy. |
| 1. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. | (A) is True but (R) is False. |
| 4. | (A) is False but (R) is True. |
Subtopic: Shell & Subshell |
92%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Select Question Set:
© 2025 GoodEd Technologies Pvt. Ltd.